VOLUME DELL' IPERSFERA

Vorrei intrattenervi su un argomento di pubblica inutilità, ma divertente. Il volume dell'Ipersfera.

Prima di definire l'ipersfera, richiamiamo alcune nozioni "elementari" che tutti noi ricordiamo dalle scuole elementari e dalle scuole medie.

Supponiamo di avere una retta orientata, un punto O detto origine, ed un segmento di lunghezza unitaria. Fissate queste tre entità geometriche, esiste una corrispondenza biunivoca tra i numeri reali ed i punti sulla retta. Quindi, ad esempio, al numero 2.3 corrisponderà un punto (in figura, il punto A), al numero √2=1.414.... corrisponderà il punto B. Inoltre, a qualsiasi punto P della retta corrisponde uno ed un solo numero (in figura, il numero 5.5)

Stiamo lavorando ad una dimensione. La misura di qualsiasi segmento OO' è data dal rapporto tra la sua lunghezza e la lunghezza di riferimento. Chiamiamo questa misura "Volume ad una dimensione", oppure V1  . Ovviamente sappiamo che V1  è la lunghezza del segmento. Ora poniamoci la domanda: se r è un valore reale positivo, quanto misura il luogo dei punti la cui distanza dall'origine è minore o uguale ad r? Ovviamente questo luogo dei punti in UNA DIMENSIONE è il segmento che va dal punto R1 (-r) al punto R2 (r). Questo luogo dei punti misura quindi 2r. Il segmento R1R2 così definito è l'ipersfera nella dimensione 1. 

Quindi, l'ipersfera di raggio r ad una dimensione ha volume

                       V1 = 2r

Aggiungiamo una dimensione. Andiamo sul piano. Abbiamo studiato alla scuola media che, analogamente al caso ad una dimensione, se fissiamo una COPPIA di assi orientati ortogonali (chiamiamoli asse x1 ed asse x2) che si intersecano in un'origine O, e fissiamo un segmento che è un'unità di misura, allora esisterà una corrispondenza biunivoca tra COPPIE di numeri reali e punti sul piano. Questa coppia di numeri reali viene detta coppia di coordinate cartesiane. e si indica tra parentesi. Così, alla coppia (a1,a2) corrisponderà il punto A, e qualsiasi punto P avrà come corrispondenza la coppia (x1,x2).

In due dimensioni, la misura di qualsiasi figura nel piano è il rapporto tra la superficie della figura e la superficie unitaria, cioè il quadrato del segmento unitario.  Chiamiamo questa misura "Volume a due dimensioni", oppure V2  . Ovviamente sappiamo che V2  è una superficie.

Ora poniamoci la stessa domanda che ci siamo posti ad una dimensione: se r è un valore reale positivo, quanto misura il luogo dei punti del piano la cui distanza dall'origine è minore o uguale ad r? Questo luogo dei punti in DUE DIMENSIONI è ovviamente il cerchio con centro nell'origine O e raggio r. 

Il cerchio è quindi l'ipersfera in DUE DIMENSIONI. Tutti sappiamo che questa misura vale πr². Questa misura è il volume dell'ipersfera di raggio r (comunemente diremmo : l'area del cerchio di raggio r) e vale

V2 = πr²

Abbiamo fino ad ora trovato che ad una dimensione il volume dell'ipersfera è 2 volte il suo raggio, a due dimensioni è π volte il quadrato di raggio r.

Andiamo a tre dimensioni. Dalla retta siamo passati al piano. Ora dal piano passiamo allo spazio. Analogamente a quanto fatto nel piano, se fissiamo una TERNA di assi orientati ortogonali (chiamiamoli asse x1, asse x2 ed asse x3) ognuno agli altri due, che si intersecano in un'origine O e fissiamo l'unità di misura, allora esisterà una corrispondenza biunivoca tra TERNE ORDINATE di numeri reali e punti nello spazio. Questa terna di numeri reali viene detta terna di coordinate cartesiane. e si indica tra parentesi. Così, alla terna (a1,a2,a3) corrisponderà il punto A, e qualsiasi punto P avrà come corrispondenza la terna (x1,x2,x3). 

In tre dimensioni, la misura di qualsiasi figura nello spazio è il rapporto tra il volume della figura ed il volume di lato unitario, cioè il cubo del segmento unitario.  Chiamiamo questa misura "Volume a tre dimensioni", oppure V3 . In tre dimensioni, V3 è quello che anche classicamente chiamiamo "volume".

Stessa domanda:

se r è un valore reale positivo, quanto misura il luogo dei punti dello spazio la cui distanza dall'origine è minore o uguale ad r? Ovviamente questo luogo dei punti in TRE DIMENSIONI è la sfera con centro nell'origine O e raggio r. 

Tutti sappiamo che questa misura vale 4/3πr³. Questa misura è il volume dell'ipersfera di raggio r (comunemente diremmo : il volume della sfera di raggio r) e vale 4/3πr².

Riepilogando, per le dimensioni 1, 2, 3, abbiamo trovato i seguenti volumi di ipersfere:

V1 = 2 r

V2 = π r²

V3 = 4/3π r³ 

Quanto scritto fino ad ora è roba nota più o meno a tutti.

Ma adesso la domanda che ci poniamo è: come continua la serie di numeri 2, π, 4/3π ...?

Ha senso continuare a più dimensioni?

I matematici dicono che ha senso. E allora proviamoci. Abbiamo visto che l'ipersfera ad una dimensione è un segmento, l'ipersfera a due dimensioni è un cerchio, l'ipersfera a tre dimensioni è la classica sfera. Logicamente è possibile estendere il concetto alla quarta, alla quinta, all'm-esima dimensione, e definire in Rᵐ l'ipersfera di raggio r come il luogo geometrico dei punti P(x1,x2,x3,...xm) tali che la distanza dall'origine O è minore di r.

Ma come si calcola la distanza di un punto P(x1,x2,x3,...xm) dall'origine ?

Per m=1 OP= |x1|, ma anche √x1²

Per m=2 OP= √(x1²+x2²), dal teorema di Pitagora.

Per m=3 OP= √(x1²+x2²+x3²).
Analogamente, per qualsiasi m, se P(x1,x2,x3,...xm), allora 
OP  = √(x1²+x2²+x3²+....+xm²)

Qual è quindi, nello spazio ad m dimensioni Rᵐ, il volume dell'ipersfera di raggio r?
E' chiaro che sarà una costante per rᵐ.
Abbiamo visto che per m=1 la costante è 2, per m=2 la costante è π, per m=3 la costante è 4/3π. Cerchiamo lo sviluppo della serie delle costanti, in funzione della dimensione.

Per far questo, occorre capire come si passa da una dimensione alla successiva.

Consideriamo come da m=1 si passa ad m=2.

L'area del cerchio si ottiene sommando i rettangolini di base B ed altezza H, come in figura.

Ovviamente, più piccoli sono i rettangoli considerati, cioè migliore è la "risoluzione" per approssimare il cerchio, più questa somma di aree di rettangoli si avvicinerà al'area del semicerchio. (vedi figura)

Al, limite, quando questi rettangolini diventano piccolissimi, la sommatoria converge verso un valore unico, chiamato INTEGRALE dell'area dei rettangoli, dove l'angolo va da 0 (rettangolo largo in basso) all'angolo retto (rettangolo piccolissimo in alto). La formula che scriverò ora non è intuitiva. E' importante tenere in mente un fatto. Dell'elemento infinitesimo, la BASE è legata al volume della dimensione precedente (V1=2r), l'altezza, CHE E' L'ELEMENTO CHE AGGIUNGE LA DIMENSIONE, E' SEMPRE R cos (theta) dtheta. Otteniamo quindi:

In altre parole, il valore di quest'integrale che è l'area dell'ipersfera per m=2, è legato al valore del volume dell'ipersfera per m=1. Il fattore di proporzionalità è questo numero

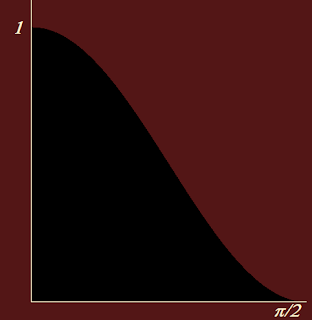
Questo numero è, per definizione, l'area nera della figura successiva.

Questo valore è calcolabile abbastanza semplicemente. Infatti risulta:

In definitiva:

che mostra il legame tra il volume dell'ipersfera con m=1 (lunghezza del segmento) ed il volume dell'ipersfera con m=2 (area del cerchio).

Vediamo come si passa da m=2 ad m=3

Il volume della sfera si ottiene sommando i cilindretti di base B ed altezza H, come in figura.

Analogamente al caso bidimensionale, più i cilindretti sono sottili, più ci avviciniamo al volune reale della sfera.

Ovviamente, mentre nel caso del cerchio (V2) la base è il segmento (V1), nel caso della sfera (V3), la base è il cerchio (V2).
Abbiamo già capito che questo passaggio al limite si chiama integrale della funzione base per altezza infinitesima. Abbiamo quindi che:

dove

quindi:

Osserviamo che abbiamo trovato la regola che lega il volume dell'ipersfera nella dimensione m a quello dell'ipersfera nella dimensione ad m-1. Infatti, abbiamo visto che

Non è difficile intuire che, in generale:

Infatti, il volume dell'ipersfera Vm è ottenuto, per come abbiamo visto, dalla somma (o integrale) di basi per altezze, dove la base è:

e l'altezza aggiunge un R cos (theta) dtheta. Di conseguenza, nell'integrale, abbiamo le costanti Vm-1(R) ed R, e le parti variabili che sono l'm-esima potenza di cos (theta) e dtheta.
Per completare il calcolo, occorre quindi determinare il valore dell'integrale:

Integrando per parti otteniamo:

ma essendo

otteniamo

e quindi:

A questo punto "siamo in porto".
Possiamo infatti calcolare il volume dell'ipersfera nello spazio Rm. In questo caso, ci limitiamo alle prime 5 dimensioni, ma la continuazione è immediata:

E' interessante notare come ogni due dimensioni viene inserito un fattore Pi greco. Questo è dovuto al fatto che l'integrale del coseno, quando la dimensione è pari, contiene il pi greco. Quando è dispari, è razionale.
Ecco una tabella riassuntiva del calcolo: